Les méthodologies issues de la Data Science permettent de mieux modéliser les comportements des assurés. En se penchant sur le cas des versements libres sur les contrats d’épargne, l’étude qui suit montre comment le machine learning peut améliorer la modélisation comportementale. Il met en particulier en lumière l’intérêt de la fonction de perte et l’importance des métriques choisies pour l’analyse des résultats. Plus que sur le choix du modèle, c’est sur ces éléments, couplés à l’analyse des données et au feature engineering, que se joue la performance de la modélisation.

Introduction

Dans son étude du 14 janvier sur la transformation numérique dans le secteur français de l’assurance, l’ACPR indique que « les innovations jugées les plus prometteuses par les organismes d’assurance […] sont celles permettant de mieux collecter, valoriser et sécuriser la donnée, notamment grâce à une utilisation accrue de l’IA ». Nous avons déjà illustré cet apport de la Data Science dans la valorisation de la donnée au travers de deux cas d’usage. Le premier s’intéressait à la vente croisée d’assurance (cross selling) et s’appuyait sur l’apprentissage supervisé. Le deuxième exploitait des données open data sur les accidents de la route en France métropolitaine pour créer un zonier en s’appuyant sur un algorithme d’apprentissage non supervisé.

Pour ce troisième cas d’usage, nous abordons les versements libres sur les contrats d’épargne. Avec l’entrée en vigueur prochaine de la norme IFRS 17, leur modélisation est devenue un enjeu pour les compagnies d’assurance. En attestent les nombreux mémoires et travaux actuariels récents publiés sur le sujet. La grande majorité de ces travaux adoptent le prisme de la classification, en cherchant par exemple à prédire si un assuré est susceptible de faire un ou des versements libres dans une période donnée. Nous avons opté pour le point de vue de la régression : notre objectif sera de prédire le montant versé par un assuré au cours d’une période donnée.

Versements libres et machine learning : données utilisées

Les données utilisées sont des données assurantielles issues de trois sources de natures différentes :

  • une base renseigne les caractéristiques des contrats d’épargne concernés (par exemple la date de souscription du contrat, son éventuelle date de sortie du portefeuille, la date de naissance de l’assuré, etc),
  • des bases annuelles indiquent l’encours sur chacun des contrats,
  • et enfin des bases annuelles portent sur les versements effectués sur les contrats concernés depuis 2006.

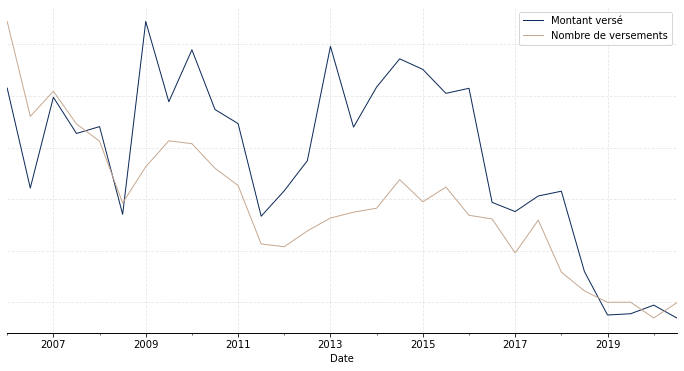
La première étape des travaux effectués, capitale, a consisté en une analyse exploratoire des données, via la réalisation de statistiques descriptives. L’objectif est de se faire une idée du phénomène étudié (ici les versements libres) et des variables importantes. C’est aussi l’occasion de conforter l’expertise métier a priori sur le sujet. Enfin, cela permet d’appréhender certains éléments clés, telle qu’une déformation temporelle par exemple. A titre illustratif, le Graphique 1 représente l’évolution temporelle du nombre total de versements (courbe en taupe) ainsi que l’évolution temporelle du montant total versé (courbe en bleu) pour le portefeuille considéré. On observe une certaine corrélation, attendue, entre les deux courbes, avec une diminution assez nette des versements à partir de 2018.

Graphique 1 : Evolution temporelle du nombre et du montant de versements libres

Evolution temporelle du nombre et du montant de versements libres

A la suite de ce travail préliminaire, nous avons mis en forme les bases de données afin de créer une base finale exploitable pour les modèles d’apprentissage automatique. Cette phase, importante, de feature engineering a pour but d’apporter le maximum de signal pour le modèle. Dans le présent cas d’usage, la variable d’intérêt que l’on cherche à prédire est le montant de versements libres effectués sur le contrat dans les six prochains mois. Et les variables créées concernent les caractéristiques de l’assuré (par exemple son âge), de son contrat (par exemple l’ancienneté) ainsi que son activité passée (par exemple l’évolution de sa provision mathématique ou son historique de versements). Même s’il paraît pertinent d’intégrer des variables exogènes (telles que le niveau de l’inflation ou l’indice de confiance des ménages) pour capter, au moins en partie, la composante conjoncturelle des versements libres, nous n’avons pas cherché ici à introduire de telles variables. Nous nous concentrons donc sur l’aspect structurel des versements libres.

Versements libres et machine learning : méthodologie adoptée

Conformément aux pratiques de la Data Science, pour valider la bonne généralisation du modèle calibré, nous avons segmenté notre base d’étude en trois :

  • une partie d’entraînement pour apprendre le modèle (64% de la base d’étude),
  • une partie de validation qui sert à estimer les méta-paramètres (16% de la base d’étude),
  • et une partie de test sur laquelle nous avons analysé les performances du modèle (20% de la base d’étude).

Nous avons ici négligé l’aspect temporel puisque le fractionnement retenu ne dépend pas du temps.

Choix de la fonction de perte

Le choix de la fonction de perte utilisée est également un élément essentiel de la modélisation. C’est cette fonction qui sera minimisée par l’algorithme selon la logique de « minimisation du risque empirique » propre à l’apprentissage automatique. Classiquement, sur des problèmes de régression comme c’est le cas ici, la fonction de perte quadratique est utilisée. C’est une fonction de la forme

    \[ L_{MSE}(y, \widehat{y}) = (\widehat{y} - y)^{2}, \]

où y est la valeur à prédire et \widehat{y} la valeur prédite par le modèle. Ce choix n’est pourtant pas toujours optimal. Dans notre cas d’usage en particulier, nous cherchons à prédire le montant de versements libres pour le prochain semestre. Or, pour de nombreux contrats, ce montant est nul (de nombreux assurés ne feront pas de versement sur leur contrat). On a donc une masse importante en 0 qui peut fausser les résultats en tirant les résultats vers 0. Dans ce cas, il semble intéressant de travailler plutôt avec la fonction de perte Tweedie définie par

    \[ L_{Tweedie}(y, \widehat{y}, \lambda) = \frac{e^{\widehat{y}(2 - \lambda)}}{2 - \lambda} - y \cdot \frac{e^{\widehat{y}(1 - \lambda)}}{1 - \lambda}, \]

avec \lambda compris entre 0 et 1. Cette fonction est liée à la famille de distributions de probabilités qui porte le même nom et qui inclut en particulier des distributions avec une masse positive en zéro et continue par ailleurs (Poisson-Gamma par exemple). C’est une sous-classe de la famille exponentielle, régulièrement utilisée dans le cadre des GLM par exemple.

Le modèle que nous avons utilisé est basé sur l’algorithme CatBoost. Ce modèle, au-delà de ses très bonnes performances de manière générale (voir par exemple le benchmark sur https://catboost.ai/), est particulièrement intéressant dans sa gestion des variables catégorielles qu’il n’est pas nécessaire de transformer en amont, ce sujet restant complexe en Data Science.

Nous avons testé deux variantes : une variante « RMSE » (le package CatBoost utilise le RMSE plutôt que le MSE en fonction de perte) et une variante « Tweedie », pour mesurer l’apport du choix de la fonction de perte dans la modélisation.

Quelle amélioration dans la prédiction des versements libres ?

Après avoir calibré les deux variantes, nous avons analysé leur performance sur la base de test. Le montant total prédit via la variante « Tweedie » est 0,71% supérieur au montant total réel ; via la variante « RMSE », il est 0,35% inférieur. L’erreur logarithmique quadratique moyenne est de 45,4 pour la variante « Tweedie » et 51,6 pour la variante « RMSE ». Au global, les résultats sont très bons et très proches. Ces métriques d’analyse ne sont cependant pas les plus adaptées : elles ne disent rien de l’adéquation du modèle à une maille individuelle. Or, l’objectif de la modélisation n’est pas simplement de déterminer le montant correct de versements libres au global, mais aussi de les ventiler de manière adéquate selon des variables d’intérêt, par exemple l’âge, l’ancienneté ou la provision mathématique (PM).

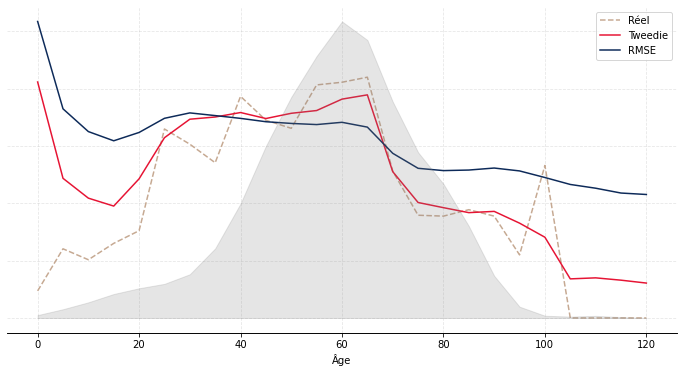
Nous avons donc représenté sur le Graphique 2 le montant moyen réel et prédit des versements libres sur la base de test par âge (Graphique 2a), ancienneté (Graphique 2b) et PM (Graphique 2c). Les courbes taupe en pointillé correspondent au réel, les courbes en bleu aux prédictions issues de l’approche « RMSE » et les courbes rouges aux prédictions issues de l’approche « Tweedie ». Les aires en gris correspondent à l’exposition.

De façon générale, on observe une meilleure adéquation de l’approche « Tweedie ». C’est particulièrement visible par ancienneté (resp. par PM), où l’approche « RMSE » a tendance sous-estimer (resp. surestimer) le montant moyen versé au début puis à le surestimer (resp. sous-estimer) ensuite. Par âge, l’approche « RMSE » a tendance à le surestimer aux âges extrêmes et à le sous-estimer aux âges intermédiaires ; l’approche « Tweedie » est performante hormis aux âges faibles (avant 20 ans) où l’exposition est néanmoins moindre.

Graphique 2 : Résultats du modèle sur la base de test

 

Versements libres - Résultats par âge

(a) : Résultats par âge

 

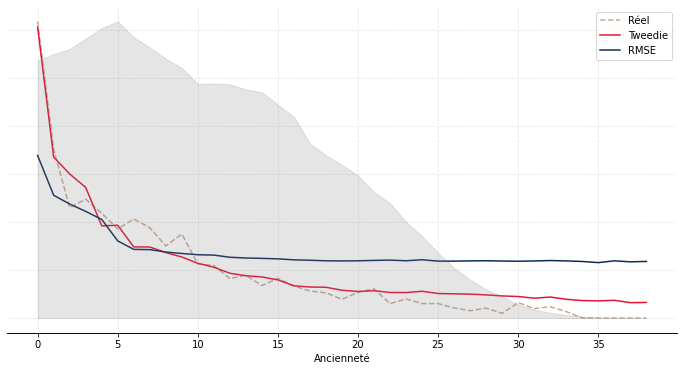
Versements libres - résultats par ancienneté

(b) : Résultats par ancienneté

 

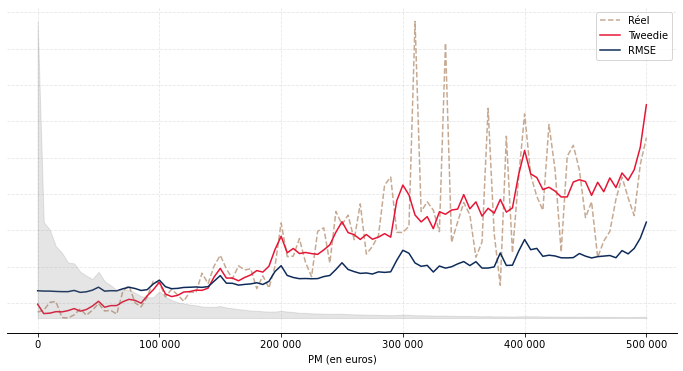
Versements libres - résultats selon provision mathématique

(c) : Résultats par PM

Conclusion

En s’appuyant sur un cas d’usage d’actualité, à savoir les versements libres sur les contrats d’épargne, ce travail a montré comment les méthodologies issues de la Data Science pouvaient améliorer la modélisation comportementale. Il a en particulier permis d’insister tant sur l’intérêt de la fonction de perte que sur l’importance des métriques choisies pour l’analyse des résultats. Plus que sur le choix du modèle, c’est sur ces éléments, couplés à l’analyse des données et au feature engineering, que se joue la performance de la modélisation.