Comment améliorer la connaissance des assurés grâce au machine learning ? – Cas d’usage #1 – le cross selling

Introduction

La compréhension des mécanismes décisionnels des assurés est un enjeu majeur en assurance. Les actuaires l’abordent généralement par le biais de lois comportementales qui précisent, en fonction de certaines variables (ancienneté, niveau de provision mathématique…), la probabilité de réalisation d’un événement (rachat d’un contrat d’épargne ou versement de primes complémentaires par exemple).

Si ces lois sont utiles pour évaluer les engagements de l’assureur, valoriser ses portefeuilles d’affaires ou mesurer ses besoins en capital, elles s’appuient sur un nombre de variables souvent limité en raison des contraintes techniques de leur utilisation. Elles ne permettent donc pas forcément une modélisation fine du risque sous-jacent. Cette modélisation fine pourrait pourtant être intéressante dans un contexte marketing. C’est notamment le cas pour cibler les clients ou prospects les plus susceptibles d’être intéressés par l’offre d’une campagne commerciale.

Dans cet article, nous montrons comment les méthodologies issues de la Data Science, et en particulier les algorithmes d’apprentissage automatique, peuvent aider à mettre en place des ciblages marketing efficaces. Ce point est d’ailleurs mentionné par l’ACPR ([1]) qui indique, dans son étude sur la transformation numérique dans le secteur français de l’assurance parue le 14 janvier 2022, que « l’IA permet d’augmenter les capacités d’ « acquisition » (meilleur ciblage des nouveaux clients) ».

Pour ce cas d’usage, nous avons utilisé un jeu de données Kaggle de vente croisée en assurance pour déterminer les assurés qui bénéficient d’une assurance santé et sont susceptibles d’être intéressés par une offre d’assurance auto.

Visionnez le replay de notre webinar : « Modélisation : comment faire parler la donnée grâce au machine learning ? »

Cross selling et modélisation par machine learning

Le jeu de données utilisé comporte 381 109 lignes et 10 variables : l’âge de l’assuré, son sexe, s’il possède ou non le permis de conduire, son code région, s’il a déjà une assurance auto ou non, l’âge de son véhicule, s’il a déjà eu des dommages auto ou non, la prime annuelle qu’il doit payer, le canal de contact privilégié de cet assuré par la compagnie, son ancienneté dans celle-ci.

Analyse de statistiques descriptives

1ère étape, classique mais néanmoins importante : analyse de statistiques descriptives, pour se faire une première idée de l’impact des variables ainsi que leur corrélation. Idéalement, lorsque c’est possible, c’est aussi l’occasion de conforter l’expertise métier a priori sur le sujet. A titre illustratif, le Graphique 1 superpose le profil du portefeuille santé et le taux de réponse à une campagne marketing en auto en fonction de l’âge. On observe que l’exposition du portefeuille santé se concentre sur les âges inférieurs à 30 ans, tandis que la proportion d’individus intéressés par une assurance auto est relativement faible à ces âges (autour de 5%).

Le taux de réponse est multiplié par 4 autour de 35 ans. Il est stable ensuite jusqu’à 45 ans puis diminue linéairement après cet âge. Comme pressenti, l’âge joue donc un rôle dans le présent cas d’usage.

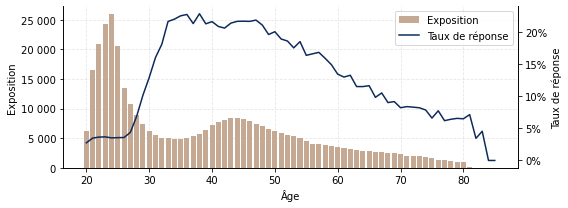
Graphique. 1 – Taux de transformation par âge.

Feature engineering

Une étape de feature engineering est souvent nécessaire par la suite. Cette étape consiste à créer ou modifier certaines variables et à gérer les valeurs manquantes ou erronées. Dans le présent cas d’usage, nous nous sommes appuyés sur les variables existantes, sans chercher à en développer de nouvelles ou à en exclure certaines de la modélisation.

Modélisation

Commence ensuite la partie modélisation. Depuis quelques années, de nombreux algorithmes ont fait leur preuve dans les compétitions de Data Science, souvent à base d’arbres de décision, par exemple XGBoost (que nous utilisons ici), LightGBM ou encore CatBoost, tous 3 dérivés de l’algorithme de gradient boosting proposé par Friedman ([2], [3]) ou de réseaux de neurones.

Pour valider la bonne généralisation du modèle, il est important de bien diviser la base, a minima en 2, afin de disposer d’une partie non impliquée dans l’apprentissage. Pour le présent cas d’usage, nous avons divisé la base en 3 :

• une partie pour l’apprentissage du modèle (training dataset de 243 909 lignes ici),
• une partie non biaisée utilisée pour évaluer le modèle lors de l’ajustement des hyperparamètres (validation dataset de 60 978 lignes ici)
• et donc la dernière partie pour évaluer le modèle final (test dataset de 76 222 lignes ici).

Si la temporalité est importante, le fractionnement devra en tenir compte (par exemple en divisant la base par semestres et en utilisant le plus récent comme base de test). Nous n’avons pas pu le faire avec notre cas d’étude en raison de l’absence de date dans la base.

Choix de la fonction de perte

Autre élément important dans la mise en place du modèle : le choix de la fonction de perte. Classiquement, quand il s’agit d’un problème de classification, la logloss est retenue (c’est le cas pour cette étude). Cependant, il est parfois intéressant de retravailler cette fonction, par exemple en cas de déséquilibre fort dans la variable à prédire (imbalanced dataset). Cela n’a pas été fait ici.

Analyse de performance sur la base de test

Le modèle calibré, nous avons analysé ses performances sur la base de test. En fonction de l’objectif affiché, toutes les métriques usuelles (i.e. la matrice de confusion, la précision ou le rappel), ne sont pas forcément pertinentes à considérer. Pour le cas d’usage étudié, les métriques retenues sont :

• l’Area Under the ROC Curve ou AUC, qui indique à quel point le modèle est capable de distinguer les classes (plus l’AUC est proche de 100%, meilleur est le modèle – ici, sa valeur atteint 86% -),
• et le lift, par exemple à 1% / 5% / 10% / 20%, qui précise le taux de réponse du segment ciblé (c’est-à-dire les scores les 1% / 5% / 10% / 20% les plus élevés) rapporté au taux de réponse moyen (donc plus le lift est élevé, meilleure est la performance – les valeurs sont ici respectivement 3,8 / 3,5 / 3,3 / 3), comme indiqué sur le Graphique 2.

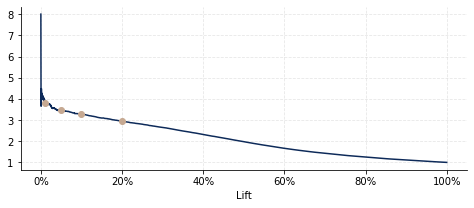
Graphique. 2 – Courbe Lift.

Analyse du modèle de machine learning

Outre la performance du modèle, son analyse revêt également un caractère primordial : d’une part parce que le régulateur, qu’il s’agisse de l’ACPR ou de la CNIL, met en garde contre les décisions non maîtrisées issues d’algorithmes « boîte noire », et d’autre part parce que la compréhension des mécanismes sous-jacents aux décisions des assurés procure un levier essentiel dans la gestion et le pilotage des décisions pour le top management. Il est donc important de définir un cadre explicatif pour le modèle retenu.

Recours au cadre SHAP

Dans cet article, nous avons utilisé le cadre SHAP (pour SHapley Additive eXplanations) proposé par Lundberg, Erion et Lee (voir à ce sujet [4], [5], [6], [7] par exemple). Le principe consiste à proposer un modèle simple pour approximer le modèle plus complexe de machine learning. Pour chaque prédiction, ce modèle simplifié s’exprime comme la somme des contributions de chacune des variables du modèle.

Pour chaque variable, cette contribution est calculée en s’appuyant sur la valeur de Shapley issue de la théorie des jeux. Ce modèle simplifié sert donc à mesurer l’impact des variables sur chaque prédiction. Evidemment, l’hypothèse d’additivité sous-jacente est forte et il convient de le garder à l’esprit lors de l’analyse des résultats. Le Graphique 3 ci-après présente les résultats obtenus en appliquant le cadre explicité ci-dessus à chacune des prédictions issues du modèle XGBoost (sur la base de test).

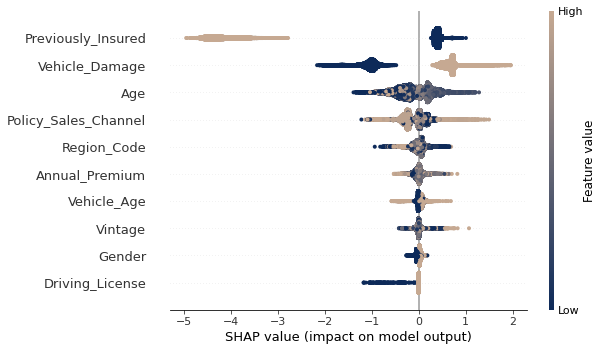
Graphique. 3 – Analyse SHAP.

Variable significative

Plusieurs informations sont ici mises en exergue. Et d’abord l’importance des variables (en fonction de leur impact sur la prédiction) : l’indicatrice d’assurance auto est la variable la plus significative au global, suivie de l’indicatrice de dommage(s) passé(s) puis de l’âge. Sur l’axe des ordonnées, un point indique sa valeur et son impact sur le modèle pour une prédiction donnée : la couleur tend vers le beige si la valeur de la variable est élevée et vers le bleu si elle est faible. La contribution de la variable se lit sur l’axe des abscisses. Si le point est à gauche du 0, la variable diminue la prédiction ; à droite, elle l’augmente. Par exemple, on observe clairement ici qu’au global, le fait d’avoir déjà une assurance auto (Previously Insured) diminue la probabilité d’une réponse positive à la campagne marketing (points beiges à gauche du 0, points bleus à droite).

Nous pouvons mener l’analyse à un niveau plus individuel, pour mettre en évidence l’explication derrière une prédiction particulière, comme dans l’exemple du Graphique 4 ci-après.

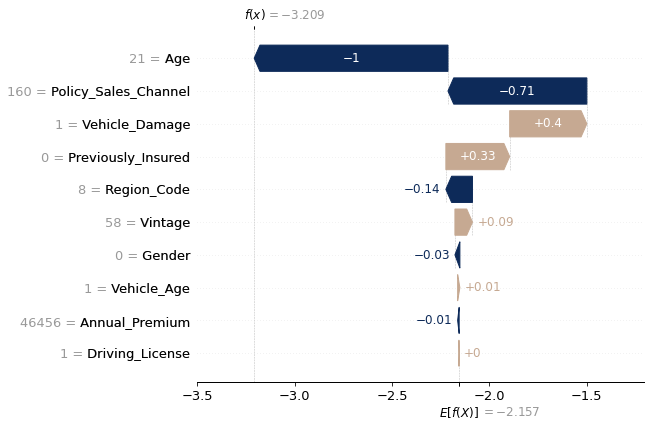
Graphique. 4 – Exemple de SHAP individuel.

Ici, le modèle part de la prédiction standard (−2,157) et corrige en fonction des variables. L’âge de l’assuré (21 ans) est ici la variable avec le plus d’impact : elle vient diminuer la prédiction de 1. Le canal de communication (dont le code est 160) est la deuxième variable la plus impactante, avec une diminution de 0,71, suivi de l’indicatrice de dommage(s) passé(s) du véhicule (ici à 1), qui augmente la prédiction de 0,4. Au global, on retrouve, avec un écart lié aux arrondis, −3, 209 ≈ −2, 157+0−0, 01+ 0, 01 − 0, 03 + 0, 09 − 0, 14 + 0, 33 + 0, 4 − 0, 71 − 1.

Cette analyse permet également d’envisager des actions ciblées selon les profils des assurés, pour optimiser les résultats des actions menées.

Gain du ciblage issu du modèle de machine learning

Dans ce cas d’usage, le gain apporté par le recours aux techniques de machine learning eu égard au coût engendré pour leur mise en place pourrait se mesurer à l’aide du ROI (Return On Investment), la mesure traditionnelle d’évaluation de la profitabilité d’un investissement.

Maximiser le taux de réponse ou minimiser les assurés contactés

Ici, nous nous sommes intéressés surtout aux gains potentiels réalisés si nous avions mené une action de ciblage sur les individus de la base de test. Deux approches possibles : soit on cherche à maximiser le taux de réponse en contactant un nombre défini d’assurés (par exemple 10 000), soit on cherche à minimiser le nombre d’assurés contactés pour arriver à un nombre de réponses cible (par exemple 2 000).

Le Graphique 5 montre l’apport direct du modèle, en présentant le nombre de transformations en fonction du nombre de personnes contactées, selon que l’on cible aléatoirement ou via le modèle.

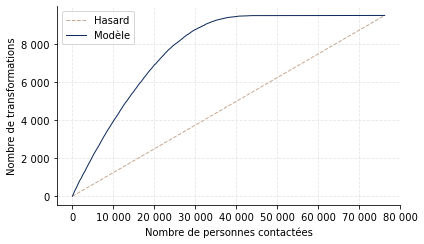
Graphique. 5 – Gains apportés par le modèle (base de test).

Le taux de réponse global est de 12, 5%. En contactant 10 000 personnes, on peut donc s’attendre à 1 250 souscriptions en ciblant aléatoirement. Et il faut contacter environ 16 000 assurés pour atteindre 2 000 souscriptions.

En utilisant le modèle et en contactant les 10 000 scores les plus élevés, on obtient 3 953 souscriptions (soit 2 703 de plus qu’aléatoirement). Pour atteindre 2 000 souscriptions, il n’y a besoin que de 4 683 contacts (soit 11 317 de moins qu’aléatoirement). En estimant la valeur d’une souscription ou le coût d’un contact supplémentaire, on en déduit alors rapidement le gain engendré par le modèle, puis le ROI en comparant au coût de sa mise en œuvre.

Conclusion

Nous avons montré, sur un cas d’usage concret, comment les méthodologies issues de la Data Science peuvent améliorer la connaissance des assurés et par extension, la vente croisée d’assurance. Plus largement, la démarche adoptée s’applique également au ciblage des individus susceptibles d’effectuer un rachat ou un versement par exemple. Elle peut donc améliorer la gestion des risques aussi bien que le marketing en plus de l’actuariat.

Pour découvrir les prochains cas d’usage :

Abonnez-vous à la Newsletter

***

Références

[1] ACPR. « Analyses et synthèses – la transformation numérique dans le secteur français de l’assurance », 2022.

[2] Jerome H. Friedman. “Stochastic gradient boosting”, Comput. Stat. Data Anal., vol. 38, no. 4, pp. 367–378, Feb. 2002.

[3] Jerome H. Friedman.“Greedy function approximation: A gradient boosting machine”, The Annals of Statistics, vol. 29, no. 5, pp. 1189 – 1232, 2001.

[4] Scott M Lundberg and Su-In Lee. “A unified approach to interpreting model predictions”, in Advances in Neural Information Processing Systems 30, I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, Eds., pp. 4765–4774. Curran Associates, Inc., 2017.

[5] Scott M. Lundberg, Gabriel Erion, Hugh Chen, Alex De-Grave, Jordan M. Prutkin, Bala Nair, Ronit Katz, Jonathan Himmelfarb, Nisha Bansal, and Su-In Lee. “From local explanations to global understanding with explainable ai for trees”, Nature Machine Intelligence, vol. 2, no. 1, pp. 2522–5839, 2020.

[6] Scott M Lundberg, Bala Nair, Monica S Vavilala, Mayumi Horibe, Michael J Eisses, Trevor Adams, David E Liston, Daniel King-Wai Low, Shu-Fang Newman, Jerry Kim, et al. “Explainable machine-learning predictions for the prevention of hypoxaemia during surgery”, Nature Biomedical Engineering, vol. 2, no. 10, pp. 749, 2018.

[7] Scott M. Lundberg, Gabriel G. Erion, and Su-In Lee. “Consistent individualized feature attribution for tree ensembles”, CoRR, vol. abs/1802.03888, 2018.