La crise que nous traversons, principalement sanitaire et économique, modifie considérablement l’exposition au risque des assureurs, aussi bien en Vie qu’en Non-vie : hausse des arrêts de travail et des défauts des entreprises, baisse des accidents de la route… Depuis 1918, aucune pandémie majeure n’a touché l’Occident, les éléments de comparaison manquent chez les assureurs à l’heure de provisionner. Les méthodes de provisionnement déterministes de type Chain-Ladder reposent en effet principalement sur les données historiques de sinistralité. Elles sont d’autant plus performantes que :
- le passé est régulier ;
- le présent et le futur sont structurellement peu différents du passé ;
- la branche considérée est peu volatile.
La qualité de l’estimation de la provision estimée par Chain-Ladder repose ainsi d’abord sur la qualité et la stabilité des données.
Face à ce constat, les assureurs peuvent être tentés, au titre des années de survenance 2019-2020, de basculer d’une méthode de Chain Ladder à celle de Bornhuetter–Ferguson : cette dernière permet de provisionner des triangles instables, par l’intégration d’une information exogène au triangle. Cette méthode consiste à utiliser un loss ratio « attendu », déterminé à l’aide de considérations exogènes au triangle. La méthode de Bornhuetter–Ferguson est ainsi une méthode adaptée à une période instable comme celle que nous traversons à cause de l’épidémie de Covid-19, mais est soumise à la détermination du Loss-ratio et notamment son dénominateur qui est le facteur d’exposition. Elle comporte donc en son sein un nouveau facteur d’aléa.
Certaines directions techniques s’orientent donc vers une autre démarche, moins connue : la méthode de Berquist & Sherman. Quels sont ses avantages dans le contexte actuel et comment l’appliquer ?
Deux méthodes sont proposées par Berquist-Sherman, en fonction de la situation de l’entreprise d’assurance :
- L’une convient en cas d’augmentation subite des PSAP (ou provisions dossier-dossier) en cette période de pandémie (augmentation des sinistres en nombre ou en sévérité) ;
- L’autre sera appliquée si ce sont les règlements de sinistres qui augmentent rapidement (en nombre ou en sévérité).
Dans la suite de cette étude, nous utiliserons les notations suivantes :
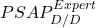 l’estimation pour un sinistre déclaré (donc ouvert/non clos) à jugement d’experts des montants de règlements qui restent à payer,
l’estimation pour un sinistre déclaré (donc ouvert/non clos) à jugement d’experts des montants de règlements qui restent à payer,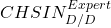 la charges des sinistres (déclarés à dire d’expert) =
la charges des sinistres (déclarés à dire d’expert) = 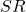 (les Sinistres réglés) +
(les Sinistres réglés) + 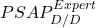 (les provisions dossier déterminés à dire d’expert).
(les provisions dossier déterminés à dire d’expert).
Méthode 1 de Berquist & Sherman : Ajustement du triangle de 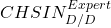 à travers celui des
à travers celui des 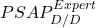
Cette méthode consiste à ajuster le triangle des ![]() dans l’optique de réduire l’effet d’une instabilité des montants de
dans l’optique de réduire l’effet d’une instabilité des montants de ![]() .
.
Étape 1 : Ajustement d’une courbe mathématique pour chaque colonne du triangle des 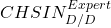
La première étape consiste à identifier une fonction mathématique qui permettrait de modéliser l’évolution des ![]() . L’ajustement d’une courbe exponentielle a été suggéré dans l’article de Berquist et Sherman, mais d’autres courbes peuvent être plus adéquates selon les données. Pour trouver la tendance associée à une courbe exponentielle, la droite des moindres carrés doit être ajustée pour chaque colonne j du triangle en passant au logarithmique :
. L’ajustement d’une courbe exponentielle a été suggéré dans l’article de Berquist et Sherman, mais d’autres courbes peuvent être plus adéquates selon les données. Pour trouver la tendance associée à une courbe exponentielle, la droite des moindres carrés doit être ajustée pour chaque colonne j du triangle en passant au logarithmique :
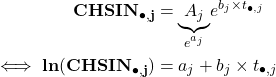
Ensuite, la tendance empirique ![]() (exprimée en %) est obtenue à partir de la formule suivante :
(exprimée en %) est obtenue à partir de la formule suivante :
![]() . En effet, l’équation ci-dessous montre la relation entre les valeurs de 2 années de survenances consécutives pour la même période de développement :
. En effet, l’équation ci-dessous montre la relation entre les valeurs de 2 années de survenances consécutives pour la même période de développement :
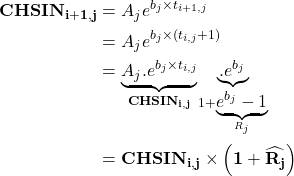
Une fois les coefficients ![]() et
et ![]() estimés et le coefficient R² (soit 1- la somme des carrés des résidus/la somme des carrés totaux ; i.e. la proportion de variance expliquée par le modèle dans la variance totale) déterminé et proche de 1 (idéalement >80%), on peut conclure qu’un modèle exponentiel est adapté à un lissage.
estimés et le coefficient R² (soit 1- la somme des carrés des résidus/la somme des carrés totaux ; i.e. la proportion de variance expliquée par le modèle dans la variance totale) déterminé et proche de 1 (idéalement >80%), on peut conclure qu’un modèle exponentiel est adapté à un lissage.
Étape 2 : Sélection d’une tendance pour le triangle des 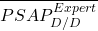 et lissage de ses diagonales
et lissage de ses diagonales
La prochaine étape consiste à ajuster le triangle des ![]() qui est obtenu en divisant chaque cellule du triangle des
qui est obtenu en divisant chaque cellule du triangle des ![]() par le nombre de sinistres déclarés ouverts afférents (c’est donc le triangle des
par le nombre de sinistres déclarés ouverts afférents (c’est donc le triangle des ![]() moyennes). L’idée est de dire que la relation entre les valeurs de 2 années de survenances consécutives pour la même période de développement est :
moyennes). L’idée est de dire que la relation entre les valeurs de 2 années de survenances consécutives pour la même période de développement est :
![]()
Cela suppose que la tendance moyenne ![]() (exprimée en %) est la même à chaque période d’évaluation, ce qui n’est pas complètement aberrant dans le cas d’un triangle de valeurs moyennes de PSAP.
(exprimée en %) est la même à chaque période d’évaluation, ce qui n’est pas complètement aberrant dans le cas d’un triangle de valeurs moyennes de PSAP.
Si à présent on suppose que le niveau des réserves reflété par les données de la dernière année calendaire d’évaluation (donc la dernière diagonale) est « correct », au sens où son utilisation est censée donner une bonne estimation des règlements non encore payés pour les sinistres déclarés, on peut donc lisser le triangle ![]() en figeant la dernière diagonale et en recalculant les plus anciennes selon la relation :
en figeant la dernière diagonale et en recalculant les plus anciennes selon la relation :
Deux décisions doivent donc être prises :
- Quelle tendance moyenne
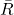 choisir?
choisir? - Quelles diagonales modifier/figer ?
Cette tendance moyenne ![]() est supposée refléter le gonflement ou le dégonflement du nombre de sinistres, notamment suite à la manifestation des facteurs externes qui motivent l’utilisation de la méthode de Berquist & Sherman. Si les triangles sont nets de réassurance, la tendance moyenne
est supposée refléter le gonflement ou le dégonflement du nombre de sinistres, notamment suite à la manifestation des facteurs externes qui motivent l’utilisation de la méthode de Berquist & Sherman. Si les triangles sont nets de réassurance, la tendance moyenne ![]() peut aussi être affectée par une modification des niveaux de rétention.
peut aussi être affectée par une modification des niveaux de rétention.
Dans leur article, Berquist & Sherman ont choisi de prendre ![]() = 15%, correspondant à un benchmark réalisé. Le marché des Lloyd’s of London estime les indemnisations au titre de 2020 entre 3 et 4,3 milliards de dollars pour ses clients dans le monde, coût pour l’assureur anglais comparable à celui du 11 Septembre 2001 (4,7 milliards) ou encore à celui des ouragans de 2017 (4,8 milliards). Ainsi, il serait intéressant, pour tout assureur souhaitant utiliser la méthode de Berquist & Sherman et subissant des répercussions semblables à celles des années de 2001 et 2017, de calculer
= 15%, correspondant à un benchmark réalisé. Le marché des Lloyd’s of London estime les indemnisations au titre de 2020 entre 3 et 4,3 milliards de dollars pour ses clients dans le monde, coût pour l’assureur anglais comparable à celui du 11 Septembre 2001 (4,7 milliards) ou encore à celui des ouragans de 2017 (4,8 milliards). Ainsi, il serait intéressant, pour tout assureur souhaitant utiliser la méthode de Berquist & Sherman et subissant des répercussions semblables à celles des années de 2001 et 2017, de calculer ![]() à partir de ses tableaux de PSAP évalués à fin 2001 et fin 2017.
à partir de ses tableaux de PSAP évalués à fin 2001 et fin 2017.
On obtient ainsi le triangle ![]() , ajusté à partir du triangle des
, ajusté à partir du triangle des ![]() , sauf pour la dernière diagonale qui est la même que celle du triangle
, sauf pour la dernière diagonale qui est la même que celle du triangle ![]() .
.
Étape 3 : Ajustement du triangle des 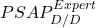
Le triangle ajusté ![]() est alors obtenu en multipliant chaque valeur du triangle
est alors obtenu en multipliant chaque valeur du triangle
![]() par le nombre de sinistres déclarés non clos afférent.
par le nombre de sinistres déclarés non clos afférent.
Étape 4 : Ajustement du triangle de la charge des sinistres déclarés
On obtient finalement le triangle ajusté des ![]() comme suit :
comme suit :
triangle ![]() = triangle
= triangle ![]() + triangle des SR
+ triangle des SR
Méthode 2 de Berquist & Sherman : Ajustement du triangle de 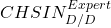 à travers celui des
à travers celui des 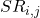 (montants cumulés de prestations payées)
(montants cumulés de prestations payées)
Étape 1 : Calcul et validation de la fiabilité du triangle 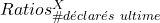 des fréquences cumulées de clôture des sinistres déclarés
des fréquences cumulées de clôture des sinistres déclarés
On définit le triangle ![]() comme étant celui des ratios « nombre cumulé
comme étant celui des ratios « nombre cumulé ![]() de sinistres clos/nombre cumulé
de sinistres clos/nombre cumulé ![]() des sinistres déclarés à l’ultime pour l’année i»,
des sinistres déclarés à l’ultime pour l’année i», ![]() étant obtenu par Chain-Ladder à partir du triangle cumulé D des sinistres déclarés cumulés.
étant obtenu par Chain-Ladder à partir du triangle cumulé D des sinistres déclarés cumulés.
En regardant chaque colonne j du triangle ![]() , une diminution du taux de clôture des sinistres sur la période j considérée peut être suspectée. En consultant l’équipe en charge des réclamations au sein de la compagnie d’assurance ou de gestionnaire tiers si les réclamations ne sont pas traitées en interne, le changement suspect dans le schéma de règlement doit être expliqué.
, une diminution du taux de clôture des sinistres sur la période j considérée peut être suspectée. En consultant l’équipe en charge des réclamations au sein de la compagnie d’assurance ou de gestionnaire tiers si les réclamations ne sont pas traitées en interne, le changement suspect dans le schéma de règlement doit être expliqué.
Étape 2 : Recherche d’une relation mathématique entre le montant cumulé de prestations payées 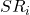 et le nombre cumulé de sinistres clos
et le nombre cumulé de sinistres clos 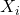 pour une année de survenance i
pour une année de survenance i
Berquist et Sherman ont utilisé une courbe exponentielle pour approcher, pour chaque année de survenance i, la relation entre ![]() le nombre cumulé de sinistres clos et
le nombre cumulé de sinistres clos et ![]() le montant cumulé des prestations payées. Par exemple, les coefficients peuvent être estimés grâce à l’équation suivante :
le montant cumulé des prestations payées. Par exemple, les coefficients peuvent être estimés grâce à l’équation suivante :
![]()
Une fois les coefficients estimés ![]() et
et ![]() en passant à une échelle logarithmique (comme à la méthode 1) et le coefficient R² suffisamment proche de 1 pour toutes les années de survenances i, on considère le modèle exponentiel adapté à un lissage.
en passant à une échelle logarithmique (comme à la méthode 1) et le coefficient R² suffisamment proche de 1 pour toutes les années de survenances i, on considère le modèle exponentiel adapté à un lissage.
Étape 3 : Ajustement du triangle SR de montants de prestations payées
On note diag(![]() ) la diagonale du triangle calculé à l’étape 1. Si l’on indice les éléments de ce vecteur de j allant de 0 à n, le jème élément de diag(
) la diagonale du triangle calculé à l’étape 1. Si l’on indice les éléments de ce vecteur de j allant de 0 à n, le jème élément de diag(![]() ) est le ratio « nombre cumulé
) est le ratio « nombre cumulé ![]() de sinistres clos/nombre
de sinistres clos/nombre ![]() de sinistres déclarés à l’ultime pour l’année n-j ».
de sinistres déclarés à l’ultime pour l’année n-j ».
Cette diagonale donne pour chaque année de développement j une fréquence cumulée, vue à la date d’évaluation (l’année n), de sinistres survenus en n-j et clos en j, rapportée aux sinistres déclarés à l’ultime pour l’année de survenance n-j.
Le triangle ajusté ![]() des nombres cumulés de sinistres clos est alors obtenu comme suit :
des nombres cumulés de sinistres clos est alors obtenu comme suit :
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \tilde{X}_{i,j} & = D_{i,n} \times \left [ diag \left ( Ratios^X_{\#d\acute{e}clar\acute{e}s~ultime} \right ) \right ]_j \\ & = D_{i,n} \times \frac{X_{n-j,j}}{D_{n-j,n}} \\ & = \mathbf { X_{n-j,j} \times \frac{D_{i,n}}{D_{n-j,n}}} \end{split} \end{equation*}](https://seabird-consultants.eu/wp-content/ql-cache/quicklatex.com-83ab11dcb595b2279e43cee76fde30e0_l3.png)
On constate que ce lissage met en jeu ![]() (appartenant à la diagonale du triangle X) quelle que soit la ligne de
(appartenant à la diagonale du triangle X) quelle que soit la ligne de ![]() . Autrement dit, à l’instar de la méthode 1, cette méthode de lissage consiste à partir de la dernière diagonale, ici celle du triangle X, pour reconstituer les diagonales plus anciennes.
. Autrement dit, à l’instar de la méthode 1, cette méthode de lissage consiste à partir de la dernière diagonale, ici celle du triangle X, pour reconstituer les diagonales plus anciennes.
En effet, les éléments ![]() et
et ![]() des dernières diagonales respectivement après et avant ajustement sont caractérisés par l’égalité suivante :
des dernières diagonales respectivement après et avant ajustement sont caractérisés par l’égalité suivante :
![Rendered by QuickLaTeX.com \tilde{X}_{n-j,j} = D_{n-j,n} \times \left [ diag \left ( Ratios^X_{\#d\acute{e}clar\acute{e}s ~ ultime} \right ) \right ]_j = D_{n-j,n} \times \frac{X_{n-j,j}}{D_{n-j,n}}=\mathbf{X_{n-j,j}}](https://seabird-consultants.eu/wp-content/ql-cache/quicklatex.com-d34fe295173142769319495933de2658_l3.png)
Alors que la méthode 1 reconstituait les diagonales les plus anciennes (pour le triangle des PSAP moyennes) en partant de la dernière que l’on multiplie récursivement grâce à un coefficient ![]() , cette fois-ci la multiplication se fait par un coefficient
, cette fois-ci la multiplication se fait par un coefficient ![]() qui dépend de i et de j. Le triangle ajusté
qui dépend de i et de j. Le triangle ajusté ![]() des montants de prestations payées cumulés est finalement obtenu en appliquant la formule suivante :
des montants de prestations payées cumulés est finalement obtenu en appliquant la formule suivante :
![]()
en utilisant les coefficients précédemment estimés à l’étape 1 par année de survenance i.
Il y a deux donc 2 décisions à prendre :
- La première concerne la sélection d’un schéma de fréquences cumulées de clôtures de sinistres
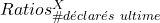 utilisé pour l’ajustement du triangle X des nombres cumulés de sinistres clos.
utilisé pour l’ajustement du triangle X des nombres cumulés de sinistres clos. - La seconde concerne la sélection des équations utilisées pour approximer la relation entre les montants cumulés de prestations payées
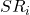 et les nombres cumulés de sinistres clos
et les nombres cumulés de sinistres clos 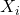 .
.
Étape 4 : Ajustement du triangle de la charges des sinistres déclarés
***
Implémentation de la méthode sur un portefeuille de sinistre
Nous avons voulu tester cette méthode en partant d’un portefeuille de sinistre relatifs à la garantie faute professionnelle médicale (méthode 1) et pour la RC automobile (méthode 2).
Méthode 1
On constate une nette diminution des charges ultimes, donc des provisions, grâce au lissage de Berquist & Sherman, surtout pour les années intermédiaires, celles dont les diagonales respectives sont les plus élevées. Ainsi, ce lissage sous-entend qu’il y avait sur-provisionnement avant son usage, et permet donc de le corriger.
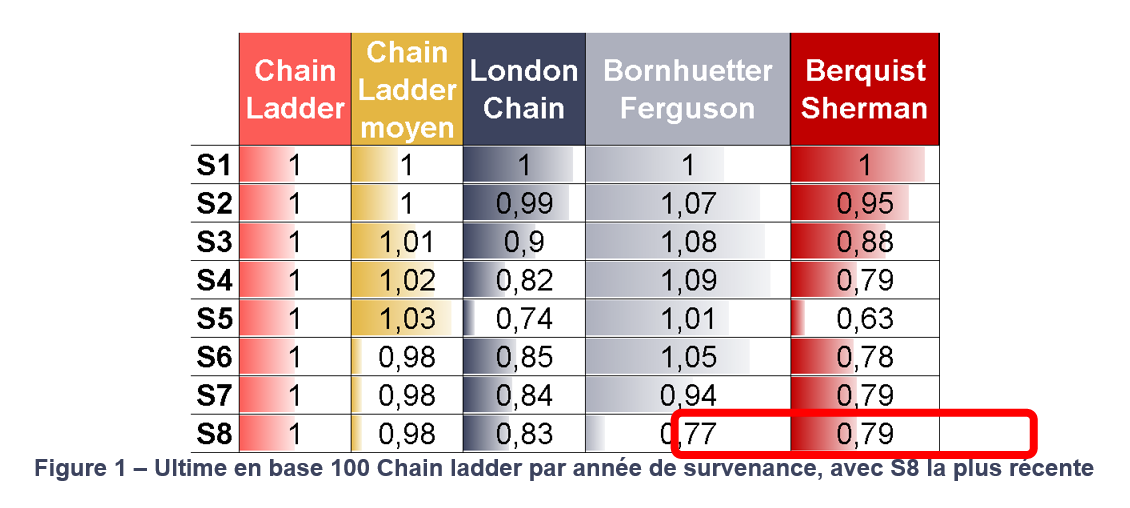
Méthode 2
Des résultats similaires sont obtenus sur ce second portefeuille en utilisant la seconde méthode, puisqu’il ressort de ce tableau que l’année de survenance la plus récente (S8) a des niveaux de provisionnement avec les méthodes classique bien supérieurs aux niveaux de provisionnement trouvés avec Berquist Sherman ou Bornhuetter Ferguson.
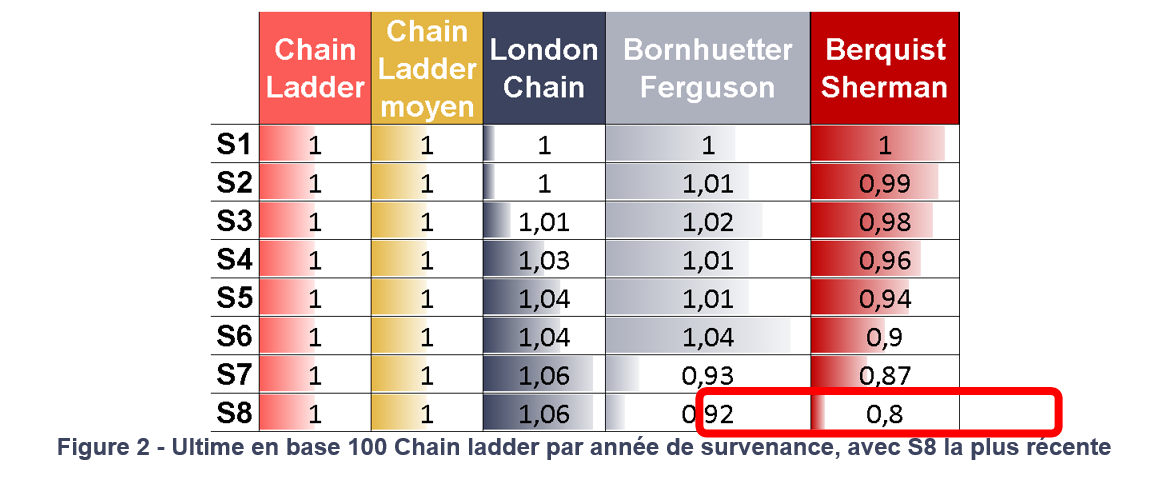
Il ressort de l’application de ces deux méthodes que Berquist Sherman et Bornhuetter-Ferguson donnent des résultats similaires pour les années de survenance récentes. L’utilisation de cette méthode dans notre portefeuille est donc pertinente, car elle permet de ne pas être pénalisé par une sur-sinistralité de la dernière survenance.
Conclusion
La méthode de Berquist Sherman est encore peu connue en France, mais la crise du Covid 19 devrait la mettre plus en lumière. Son utilisation, comme toute méthode, se doit d’être justifiée : pour ce faire, il est primordial pour les actuaires d’échanger avec les experts en règlements de sinistres pour s’assurer de la bonne compréhension des données fournies et de la justesse de leurs analyses.
Les actuaires provisionnement doivent ainsi pouvoir détecter un changement dans l’environnement et en tenir compte dans la détermination des pertes finales, l’estimation des sinistres impayés ultimes n’étant pas une tâche mécanique, et un jugement actuariel est nécessaire.
Les travaux de provisionnement sont un peu plus complexes que les méthodes habituelles, mais permettent à la fois de
- s’affranchir des limites des méthodes de Chain Ladder ou London Chain, où les années de survenance récentes peuvent peser très lourd dans l’ultime,
- valider les travaux de provisionnement de type Bornhuetter Ferguson, très utilisés pour les années de survenance récentes.
A l’heure où les directions techniques se doivent, plus que jamais, de justifier leurs niveaux d’ultime, l’application de cette méthode nous paraît opportune, car permettant de répondre aux légitimes questions des directions financière et équipes de contrôle.